Exponential function

This article is about the function f(x) = e^x and its generalizations. For functions of the form f(x) = x^r, see Power function. For the bivariate function f(x,y) = x^y, see Exponentiation. For the representation of scientific numbers, see E notation.

Exponential
The natural exponential function along part of the real axis
General information
General definition	$\exp z=e^{z}$
Domain, codomain and image
Domain	$\mathbb {C}$
Image	${\begin{cases}(0,\infty )&{\text{for }}z\in \mathbb {R} \\\mathbb {C} \setminus \{0\}&{\text{for }}z\in \mathbb {C} \end{cases}}$
Specific values
At zero	1
Value at 1	e
Specific features
Fixed point	−Wn(−1) for $n\in \mathbb {Z}$
Related functions
Reciprocal	$\exp(-z)$
Inverse	Natural logarithm, Complex logarithm
Derivative	$\exp '\!z=\exp z$
Antiderivative	$\int \exp z\,dz=\exp z+C$
Series definition
Taylor series	$\exp z=\sum _{n=0}^{\infty }{\frac {z^{n}}{n!}}$

Exponential functions with bases 2 and 1/2

In mathematics, the exponential function is the unique real function which maps zero to one and has a derivative equal to its value. The exponential of a variable ⁠$x$⁠ is denoted ⁠$\exp x$⁠ or ⁠$e^{x}$⁠, with the two notations used interchangeably. It is called exponential because its argument can be seen as an exponent to which a constant number e ≈ 2.718, the base, is raised. There are several other definitions of the exponential function, which are all equivalent although being of very different nature.

The exponential function converts sums to products: it maps the additive identity 0 to the multiplicative identity 1, and the exponential of a sum is equal to the product of separate exponentials, ⁠$\exp(x+y)=\exp x\cdot \exp y$⁠. Its inverse function, the natural logarithm, ⁠$\ln$⁠ or ⁠$\log$⁠, converts products to sums: ⁠$\ln(x\cdot y)=\ln x+\ln y$⁠.

Other functions of the general form ⁠$f(x)=b^{x}$⁠, with base ⁠$b$⁠, are also commonly called exponential functions, and share the property of converting addition to multiplication, ⁠$b^{x+y}=b^{x}\cdot b^{y}$⁠. Where these two meanings might be confused, the exponential function of base ⁠$e$⁠ is occasionally called the natural exponential function, matching the name natural logarithm. The generalization of the standard exponent notation ⁠$b^{x}$⁠ to arbitrary real numbers as exponents, is usually formally defined in terms of the exponential and natural logarithm functions, as ⁠$b^{x}=\exp(x\cdot \ln b)$⁠. The "natural" base ⁠$e=\exp 1$⁠ is the unique base satisfying the criterion that the exponential function's derivative equals its value, ⁠${\tfrac {d}{dx}}e^{x}=e^{x}$⁠, which simplifies definitions and eliminates extraneous constants when using exponential functions in calculus.

Quantities which change over time in proportion to their value, for example the balance of a bank account bearing compound interest, the size of a bacterial population, the temperature of an object relative to its environment, or the amount of a radioactive substance, can be modeled using functions of the form ⁠$y(t)=ae^{ct}$⁠, also sometimes called exponential functions; these quantities undergo exponential growth if ⁠$c$⁠ is positive or exponential decay if ⁠$c$⁠ is negative.

The exponential function can be generalized to accept a complex number as its argument. This reveals a relation between the multiplication of complex numbers and rotation in the Euclidean plane, Euler's formula ⁠$\exp i\theta =\cos \theta +i\sin \theta$⁠: the exponential of an imaginary number ⁠$i\theta$⁠ is a point on the complex unit circle at angle ⁠$\theta$⁠ from the real axis. The identities of trigonometry can thus be translated into identities involving exponentials of imaginary quantities. The complex function ⁠$z\mapsto \exp z$⁠ is a conformal map from an infinite strip of the complex plane ⁠$-\pi <\operatorname {Im} z\leq \pi$⁠ (which periodically repeats in the imaginary direction) onto the whole complex plane except for ⁠$0$⁠.

The exponential function can be even further generalized to accept other types of arguments, such as matrices and elements of Lie algebras. Some old texts refer to the exponential function as the antilogarithm.

Graph

The graph of $y=e^{x}$ is upward-sloping, and increases faster as x increases. The graph always lies above the x-axis, but becomes arbitrarily close to it for large negative x; thus, the x-axis is a horizontal asymptote. The equation ${\tfrac {d}{dx}}e^{x}=e^{x}$ means that the slope of the tangent to the graph at each point is equal to its height (its y-coordinate) at that point.

Definitions and fundamental properties

See also: Characterizations of the exponential function

There are several different definitions of the exponential function, which are all equivalent, although of very dirrerent nature.

One of the simplest definition is: The exponential function is the unique differentiable function that equal its derivative, and takes the value 1 for the value 0 of its variable.

This "conceptual" definition requires a uniqueness proof and an existence proof, but it allows an easy derivation of the main properties of the exponential function.

Uniqueness: If ⁠$f(x)$⁠ and ⁠$g(x)$⁠ are two functions satisfying the above definition, then the derivative of ⁠$f/g$⁠ is zero everywhere by the quotient rule. It follows that ⁠$g(x)$⁠ is constant, and this constant is 1 since ⁠$f(0)=g(0)=1$⁠.

The exponential function is the inverse function of the natural logarithm. The inverse function theorem implies that the natural logarithm has an inverse function, that satisfies the above definition. This is a first proof of existence. Therefore, one has

${\begin{aligned}\ln(\exp x)&=x\\\exp(\ln y)&=y\end{aligned}}$

for every real number $x$ and evey positive real number $y.$

The exponential function (in blue), and the sum of the first n + 1 terms of its power series (in red)

The exponential function is the sum of a power series: $${\begin{aligned}\exp(x)&=1+x+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+\cdots \\&=\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}},\end{aligned}}$$ where $n!$ is the factorial of n (the product of the n first positive integers). This series is absolutely convergent for every $x$ per the ratio test. So, the derivative of the sum can be computed by term-by-term derivation, and this shows that the sum of the series satisfies the above definition. This is a second existence proof, and shows, as a byproduct that the exponential function is everywhere the sum of its Maclaurin series.

The exponential satisfies the functional equation: $$\exp(x+y)=\exp(x)\cdot \exp(y).$$ This results from the uniqueness and the fact that the function $f(x)=\exp(x+y)/\exp(y)$ satisfies the above definition. It can be proved that a function that satisfies this functional equation is the exponential function if its derivative at 0 is 1 and the function is either continuous or monotonic

Positiveness: The exponential function is positive and monotonically increasing. The latter property results from the first one, since the derivative equals the function. The positiveness results for $x>0$ from the fact that all terms of the above series are positive. For $x<0,$ this results from the functional identity that implies $\exp(-x)=1/\exp(x).$

Extension of exponentiation to positive real bases: Let b be a positive real number. The exponential function and the naturel logarithm being the inverse each of the other, one has $b=\exp(\ln b).$ If n is an integer, the functional equation of the logarithm implies $$b^{n}=\exp(\ln b^{n})=\exp(n\ln b).$$ Since the right-most expression is defined if n is any real number, this allows defining ⁠$b^{x}$⁠ for every positive real number b and every real number x: $$b^{x}=\exp(x\ln b).$$ In particular, if b is the Euler's number $e=\exp(1),$ one has $\ln e=1$ (inverse function) and thus $$e^{x}=\exp(x).$$ This shows the equivalence of the two notations for the exponential function.

The exponential function is the limit $$\exp(x)=\lim _{n\to \infty }\left(1+{\frac {x}{n}}\right)^{n},$$ where $n$ takes only integer values (otherwise, the exponentiation would require the xponential function to be defined). By continuity of the logarithm, this can be proved by taking logarithms and proving $$x=\lim _{n\to \infty }\ln \left(1+{\frac {x}{n}}\right)^{n}=\lim _{n\to \infty }n\ln \left(1+{\frac {x}{n}}\right),$$ for example with Taylor's theorem.

General exponential functions

The exponential function $f(x)=e^{x}$ is sometimes called the natural exponential function to distinguish it from the other exponential functions. The study of any exponential function can easily be reduced to that of the natural exponential function, since per definition, for positive b, $$a\,b^{x}\mathrel {\stackrel {\text{def}}{=}} a\,e^{x\ln b}$$As functions of a real variable, exponential functions are uniquely characterized by the fact that the derivative of such a function is directly proportional to the value of the function. The constant of proportionality of this relationship is the natural logarithm of the base b: $${\frac {d}{dx}}a\,b^{x}={\frac {d}{dx}}a\,e^{x\ln(b)}=a\,e^{x\ln(b)}\ln(b)=a\,b^{x}\ln(b).$$Let $a>0$ be a positive coefficient. For $b>1$, the function $a\,b^{x}$ is increasing (as depicted for b = e and b = 2), because $\ln b>0$ makes the derivative always positive, and describes exponential growth. For $0<b<1$, the function is decreasing (as depicted for b = ⁠1/2⁠), and describes exponential decay. For b = 1, the function is constant.

Euler's number e = 2.71828... is the unique base for which the constant of proportionality is 1, since $\ln(e)=1$, so that the function is its own derivative: $${\frac {d}{dx}}e^{x}=e^{x}\ln(e)=e^{x}.$$

This function, also denoted as $\exp(x)$, is called the "natural exponential function", or simply "the exponential function", denoted as$$x\mapsto e^{x}\quad {\text{or}}\quad x\mapsto \exp(x).$$The former notation is commonly used for simpler exponents, while the latter is preferred when the exponent is more complicated and harder to read in a small font. Since any exponential function $f(x)=a\,b^{x}$ can be written in terms of the natural exponential, it is computationally and conceptually convenient to reduce the study of exponential functions to this particular one.

For real numbers $c,d$, a function of the form $f(x)=ab^{cx+d}$ is also an exponential function: $$ab^{cx+d}=\left(ab^{d}\right)\left(b^{c}\right)^{x}=\left(ab^{d}\right)e^{xc\ln b}.$$

Overview

The red curve is the exponential function. The black horizontal lines show where it crosses the green vertical lines.

The exponential function arises whenever a quantity grows or decays at a rate proportional to its current value. One such situation is continuously compounded interest, and in fact it was this observation that led Jacob Bernoulli in 1683 to the number $$\lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}$$ now known as e. Later, in 1697, Johann Bernoulli studied the calculus of the exponential function.

If a principal amount of 1 earns interest at an annual rate of x compounded monthly, then the interest earned each month is ⁠x/12⁠ times the current value, so each month the total value is multiplied by (1 + ⁠x/12⁠), and the value at the end of the year is (1 + ⁠x/12⁠)¹². If instead interest is compounded daily, this becomes (1 + ⁠x/365⁠)³⁶⁵. Letting the number of time intervals per year grow without bound leads to the limit definition of the exponential function, $$\exp x=\lim _{n\to \infty }\left(1+{\frac {x}{n}}\right)^{n}$$ first given by Leonhard Euler. This is one of a number of characterizations of the exponential function; others involve series or differential equations.

From any of these definitions it can be shown that e^−x is the reciprocal of e^x. For example, from the differential equation definition, e^x e^−x = 1 when x = 0 and its derivative using the product rule is e^x e^−x − e^x e^−x = 0 for all x, so e^x e^−x = 1 for all x.

From any of these definitions it can be shown that the exponential function obeys the basic exponentiation identity. For example, from the power series definition, expanded by the Binomial theorem, $$\exp(x+y)=\sum _{n=0}^{\infty }{\frac {(x+y)^{n}}{n!}}=\sum _{n=0}^{\infty }\sum _{k=0}^{n}{\frac {n!}{k!(n-k)!}}{\frac {x^{k}y^{n-k}}{n!}}=\sum _{k=0}^{\infty }\sum _{\ell =0}^{\infty }{\frac {x^{k}y^{\ell }}{k!\ell !}}=\exp x\cdot \exp y\,.$$ This justifies the exponential notation e^x for exp x.

The derivative (rate of change) of the exponential function is the exponential function itself. More generally, a function with a rate of change proportional to the function itself is expressible in terms of the exponential function. This derivative property leads to exponential growth or exponential decay.

The exponential function extends to an entire function on the complex plane. Euler's formula relates its values at purely imaginary arguments to trigonometric functions. The exponential function also has analogues for which the argument is a matrix, or even an element of a Banach algebra or a Lie algebra.

Derivatives and differential equations

The derivative of the exponential function is equal to the value of the function. From any point P on the curve (blue), let a tangent line (red), and a vertical line (green) with height h be drawn, forming a right triangle with a base b on the x-axis. Since the slope of the red tangent line (the derivative) at P is equal to the ratio of the triangle's height to the triangle's base (rise over run), and the derivative is equal to the value of the function, h must be equal to the ratio of h to b. Therefore, the base b must always be 1.

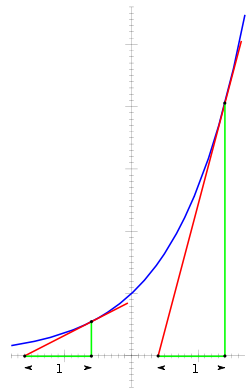
The importance of the exponential function in mathematics and the sciences stems mainly from its property as the unique function which is equal to its derivative and is equal to 1 when x = 0. That is, $${\frac {d}{dx}}e^{x}=e^{x}\quad {\text{and}}\quad e^{0}=1.$$

Functions of the form ae^x for constant a are the only functions that are equal to their derivative (by the Picard–Lindelöf theorem). Other ways of saying the same thing include:

• The slope of the graph at any point is the height of the function at that point.
• The rate of increase of the function at x is equal to the value of the function at x.
• The function solves the differential equation y′ = y.
• exp is a fixed point of derivative as a linear operator on function space.

If a variable's growth or decay rate is proportional to its size—as is the case in unlimited population growth (see Malthusian catastrophe), continuously compounded interest, or radioactive decay—then the variable can be written as a constant times an exponential function of time.

More generally, for any real constant k, a function f: R → R satisfies $f'=kf$ if and only if $f(x)=ae^{kx}$ for some constant a. The constant k is called the decay constant, disintegration constant, rate constant, or transformation constant.

Furthermore, for any differentiable function f, we find, by the chain rule: $${\frac {d}{dx}}e^{f(x)}=f'(x)\,e^{f(x)}.$$

Continued fractions for e^x

A continued fraction for e^x can be obtained via an identity of Euler: $$e^{x}=1+{\cfrac {x}{1-{\cfrac {x}{x+2-{\cfrac {2x}{x+3-{\cfrac {3x}{x+4-\ddots }}}}}}}}$$

The following generalized continued fraction for e^z converges more quickly: $$e^{z}=1+{\cfrac {2z}{2-z+{\cfrac {z^{2}}{6+{\cfrac {z^{2}}{10+{\cfrac {z^{2}}{14+\ddots }}}}}}}}$$

or, by applying the substitution z = ⁠x/y⁠: $$e^{\frac {x}{y}}=1+{\cfrac {2x}{2y-x+{\cfrac {x^{2}}{6y+{\cfrac {x^{2}}{10y+{\cfrac {x^{2}}{14y+\ddots }}}}}}}}$$ with a special case for z = 2: $$e^{2}=1+{\cfrac {4}{0+{\cfrac {2^{2}}{6+{\cfrac {2^{2}}{10+{\cfrac {2^{2}}{14+\ddots \,}}}}}}}}=7+{\cfrac {2}{5+{\cfrac {1}{7+{\cfrac {1}{9+{\cfrac {1}{11+\ddots \,}}}}}}}}$$

This formula also converges, though more slowly, for z > 2. For example: $$e^{3}=1+{\cfrac {6}{-1+{\cfrac {3^{2}}{6+{\cfrac {3^{2}}{10+{\cfrac {3^{2}}{14+\ddots \,}}}}}}}}=13+{\cfrac {54}{7+{\cfrac {9}{14+{\cfrac {9}{18+{\cfrac {9}{22+\ddots \,}}}}}}}}$$

Complex plane

See also: Euler's formula § Definitions of complex exponentiation

The exponential function e^z plotted in the complex plane from -2-2i to 2+2i

A complex plot of $z\mapsto \exp z$, with the argument $\operatorname {Arg} \exp z$ represented by varying hue. The transition from dark to light colors shows that $\left|\exp z\right|$ is increasing only to the right. The periodic horizontal bands corresponding to the same hue indicate that $z\mapsto \exp z$ is periodic in the imaginary part of $z$.

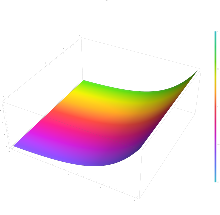
As in the real case, the exponential function can be defined on the complex plane in several equivalent forms.

The most common definition of the complex exponential function parallels the power series definition for real arguments, where the real variable is replaced by a complex one: $$\exp z:=\sum _{k=0}^{\infty }{\frac {z^{k}}{k!}}$$

Alternatively, the complex exponential function may be defined by modelling the limit definition for real arguments, but with the real variable replaced by a complex one: $$\exp z:=\lim _{n\to \infty }\left(1+{\frac {z}{n}}\right)^{n}$$

For the power series definition, term-wise multiplication of two copies of this power series in the Cauchy sense, permitted by Mertens' theorem, shows that the defining multiplicative property of exponential functions continues to hold for all complex arguments: $$\exp(w+z)=\exp w\exp z{\text{ for all }}w,z\in \mathbb {C}$$

The definition of the complex exponential function in turn leads to the appropriate definitions extending the trigonometric functions to complex arguments.

In particular, when z = it (t real), the series definition yields the expansion $$\exp(it)=\left(1-{\frac {t^{2}}{2!}}+{\frac {t^{4}}{4!}}-{\frac {t^{6}}{6!}}+\cdots \right)+i\left(t-{\frac {t^{3}}{3!}}+{\frac {t^{5}}{5!}}-{\frac {t^{7}}{7!}}+\cdots \right).$$

In this expansion, the rearrangement of the terms into real and imaginary parts is justified by the absolute convergence of the series. The real and imaginary parts of the above expression in fact correspond to the series expansions of cos t and sin t, respectively.

This correspondence provides motivation for defining cosine and sine for all complex arguments in terms of $\exp(\pm iz)$ and the equivalent power series: $${\begin{aligned}&\cos z:={\frac {\exp(iz)+\exp(-iz)}{2}}=\sum _{k=0}^{\infty }(-1)^{k}{\frac {z^{2k}}{(2k)!}},\\[5pt]{\text{and }}\quad &\sin z:={\frac {\exp(iz)-\exp(-iz)}{2i}}=\sum _{k=0}^{\infty }(-1)^{k}{\frac {z^{2k+1}}{(2k+1)!}}\end{aligned}}$$

for all ${\textstyle z\in \mathbb {C} .}$

The functions exp, cos, and sin so defined have infinite radii of convergence by the ratio test and are therefore entire functions (that is, holomorphic on $\mathbb {C}$). The range of the exponential function is $\mathbb {C} \setminus \{0\}$, while the ranges of the complex sine and cosine functions are both $\mathbb {C}$ in its entirety, in accord with Picard's theorem, which asserts that the range of a nonconstant entire function is either all of $\mathbb {C}$, or $\mathbb {C}$ excluding one lacunary value.

These definitions for the exponential and trigonometric functions lead trivially to Euler's formula: $$\exp(iz)=\cos z+i\sin z{\text{ for all }}z\in \mathbb {C} .$$

We could alternatively define the complex exponential function based on this relationship. If z = x + iy, where x and y are both real, then we could define its exponential as $$\exp z=\exp(x+iy):=(\exp x)(\cos y+i\sin y)$$ where exp, cos, and sin on the right-hand side of the definition sign are to be interpreted as functions of a real variable, previously defined by other means.

For $t\in \mathbb {R}$, the relationship ${\overline {\exp(it)}}=\exp(-it)$ holds, so that $\left|\exp(it)\right|=1$ for real $t$ and $t\mapsto \exp(it)$ maps the real line (mod 2π) to the unit circle in the complex plane. Moreover, going from $t=0$ to $t=t_{0}$, the curve defined by $\gamma (t)=\exp(it)$ traces a segment of the unit circle of length $$\int _{0}^{t_{0}}|\gamma '(t)|\,dt=\int _{0}^{t_{0}}|i\exp(it)|\,dt=t_{0},$$ starting from z = 1 in the complex plane and going counterclockwise. Based on these observations and the fact that the measure of an angle in radians is the arc length on the unit circle subtended by the angle, it is easy to see that, restricted to real arguments, the sine and cosine functions as defined above coincide with the sine and cosine functions as introduced in elementary mathematics via geometric notions.

The complex exponential function is periodic with period 2πi and $\exp(z+2\pi ik)=\exp z$ holds for all $z\in \mathbb {C} ,k\in \mathbb {Z}$.

When its domain is extended from the real line to the complex plane, the exponential function retains the following properties: $${\begin{aligned}&e^{z+w}=e^{z}e^{w}\,\\[5pt]&e^{0}=1\,\\[5pt]&e^{z}\neq 0\\[5pt]&{\frac {d}{dz}}e^{z}=e^{z}\\[5pt]&\left(e^{z}\right)^{n}=e^{nz},n\in \mathbb {Z} \end{aligned}}$$

for all ${\textstyle w,z\in \mathbb {C} .}$

Extending the natural logarithm to complex arguments yields the complex logarithm log z, which is a multivalued function.

We can then define a more general exponentiation: $$z^{w}=e^{w\log z}$$ for all complex numbers z and w. This is also a multivalued function, even when z is real. This distinction is problematic, as the multivalued functions log z and z^w are easily confused with their single-valued equivalents when substituting a real number for z. The rule about multiplying exponents for the case of positive real numbers must be modified in a multivalued context:

(e^z)^w
≠ e^zw, but rather (e^z)^w
= e^{(z + 2niπ)w} multivalued over integers n

See failure of power and logarithm identities for more about problems with combining powers.

The exponential function maps any line in the complex plane to a logarithmic spiral in the complex plane with the center at the origin. Two special cases exist: when the original line is parallel to the real axis, the resulting spiral never closes in on itself; when the original line is parallel to the imaginary axis, the resulting spiral is a circle of some radius.

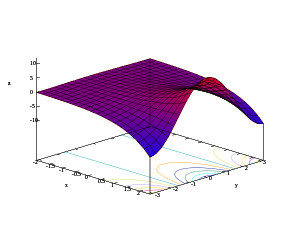
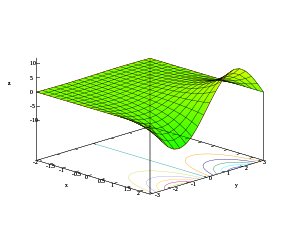
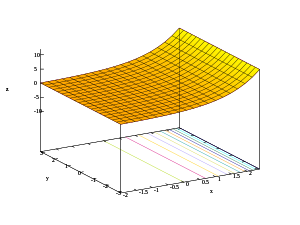
• 3D plots of real part, imaginary part, and modulus of the exponential function
• 
  z = Re(e^{x + iy})
• 
  z = Im(e^{x + iy})
• 
  z = |e^{x + iy}|

Considering the complex exponential function as a function involving four real variables: $$v+iw=\exp(x+iy)$$ the graph of the exponential function is a two-dimensional surface curving through four dimensions.

Starting with a color-coded portion of the $xy$ domain, the following are depictions of the graph as variously projected into two or three dimensions.

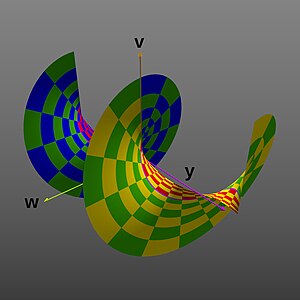
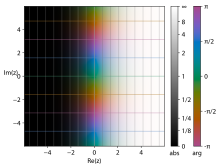
• Graphs of the complex exponential function
• 
  Checker board key:
  $x>0:\;{\text{green}}$
  $x<0:\;{\text{red}}$
  $y>0:\;{\text{yellow}}$
  $y<0:\;{\text{blue}}$
• 
  Projection onto the range complex plane (V/W). Compare to the next, perspective picture.
• 
  Projection into the $x$, $v$, and $w$ dimensions, producing a flared horn or funnel shape (envisioned as 2-D perspective image)
• 
  Projection into the $y$, $v$, and $w$ dimensions, producing a spiral shape ($y$ range extended to ±2π, again as 2-D perspective image)

The second image shows how the domain complex plane is mapped into the range complex plane:

• zero is mapped to 1
• the real $x$ axis is mapped to the positive real $v$ axis
• the imaginary $y$ axis is wrapped around the unit circle at a constant angular rate
• values with negative real parts are mapped inside the unit circle
• values with positive real parts are mapped outside of the unit circle
• values with a constant real part are mapped to circles centered at zero
• values with a constant imaginary part are mapped to rays extending from zero

The third and fourth images show how the graph in the second image extends into one of the other two dimensions not shown in the second image.

The third image shows the graph extended along the real $x$ axis. It shows the graph is a surface of revolution about the $x$ axis of the graph of the real exponential function, producing a horn or funnel shape.

The fourth image shows the graph extended along the imaginary $y$ axis. It shows that the graph's surface for positive and negative $y$ values doesn't really meet along the negative real $v$ axis, but instead forms a spiral surface about the $y$ axis. Because its $y$ values have been extended to ±2π, this image also better depicts the 2π periodicity in the imaginary $y$ value.

Computation of a^b where both a and b are complex

Main article: Exponentiation

Complex exponentiation a^b can be defined by converting a to polar coordinates and using the identity e^{b ln a} = a^b: $$a^{b}=e^{b\ln a}=e^{b\ln |a|+ib\theta }$$

with $\theta$ being an argument of $a$. However, when b is not an integer, this function is multivalued, because θ is not unique (see Exponentiation § Failure of power and logarithm identities). The quotient $0^{b}$ cannot be defined in this way since $\log 0$ is not defined. The choice of the principal value of $a^{b}$ satisfies $-\pi <\theta \leq \pi$, and this also defines the principal value of $\log a$.

Power functions and exponential function with a complex base

Given a complex number $b$ and once we have defined the principal value of $z^{b}$, we may define the single-valued functions $f(z)=z^{b}$ (known as the power function) and $g(z)=b^{z}$, which is similiar to the exponential function but the base can be a complex number. If $b$ is not an integer, then $f$ has discontinuities at negative reals, since $f(z)=e^{b\ln z}$ and this follows from the fact that the complex logarithm function is discontinuous at the negative reals. The Maclaurin series of function $f(1+z)$ is given by $$f(1+z)=\sum _{k=0}^{\infty }{\frac {b(b-1)...(b-k+1)}{k!}}z^{k}=1+bz+{\frac {b(b-1)}{2}}z^{2}+\cdots ,\qquad |z|<1.$$ This is known as the binomial series. In addition, if $b$ has a positive real part, then the series converges absolutely for $z=-1$, and the limit of $f(1+z)$ also exists as $z\to -1$ within the unit circle and is equal to $0$, so we may also define $0^{b}:=\lim _{z\to -1}f(1+z)=0$. If $b$ has a non-positive real part and $b\neq 0$ then the series diverges, so $0^{b}$ remains undefined. The expression $0^{0}$ is left undefined because it is an indeterminate form in calculus. The function $g$ defined here is holomorphic everywhere in the complex plane, and thus it is entire. The Maclaurin series of $g$ is given by $$g(z)=b^{z}=e^{z\ln b}=\sum _{k=0}^{\infty }{\frac {(\log b)^{k}}{k!}}z^{k}.$$

Matrices and Banach algebras

The power series definition of the exponential function makes sense for square matrices (for which the function is called the matrix exponential) and more generally in any unital Banach algebra B. In this setting, e⁰ = 1, and e^x is invertible with inverse e^−x for any x in B. If xy = yx, then e^{x + y} = e^xe^y, but this identity can fail for noncommuting x and y.

Some alternative definitions lead to the same function. For instance, e^x can be defined as $$\lim _{n\to \infty }\left(1+{\frac {x}{n}}\right)^{n}.$$

Or e^x can be defined as f_x(1), where f_x : R → B is the solution to the differential equation ⁠df_x/dt⁠(t) = x f_x(t), with initial condition f_x(0) = 1; it follows that f_x(t) = e^tx for every t in R.

Lie algebras

Given a Lie group G and its associated Lie algebra ${\mathfrak {g}}$, the exponential map is a map ${\mathfrak {g}}$ ↦ G satisfying similar properties. In fact, since R is the Lie algebra of the Lie group of all positive real numbers under multiplication, the ordinary exponential function for real arguments is a special case of the Lie algebra situation. Similarly, since the Lie group GL(n,R) of invertible n × n matrices has as Lie algebra M(n,R), the space of all n × n matrices, the exponential function for square matrices is a special case of the Lie algebra exponential map.

The identity $\exp(x+y)=\exp(x)\exp(y)$ can fail for Lie algebra elements x and y that do not commute; the Baker–Campbell–Hausdorff formula supplies the necessary correction terms.

Transcendency

The function e^z is not in the rational function ring $\mathbb {C} (z)$: it is not the quotient of two polynomials with complex coefficients.

If a₁, ..., a_n are distinct complex numbers, then e^a₁z, ..., e^a_nz are linearly independent over $\mathbb {C} (z)$, and hence e^z is transcendental over $\mathbb {C} (z)$.

Computation

The Taylor series definition above is generally efficient for computing (an approximation of) $e^{x}$. However, when computing near the argument $x=0$, the result will be close to 1, and computing the value of the difference $e^{x}-1$ with floating-point arithmetic may lead to the loss of (possibly all) significant figures, producing a large relative error, possibly even a meaningless result.

Following a proposal by William Kahan, it may thus be useful to have a dedicated routine, often called expm1, which computes e^x − 1 directly, bypassing computation of e^x. For example, one may use the Taylor series: $$e^{x}-1=x+{\frac {x^{2}}{2}}+{\frac {x^{3}}{6}}+\cdots +{\frac {x^{n}}{n!}}+\cdots .$$

This was first implemented in 1979 in the Hewlett-Packard HP-41C calculator, and provided by several calculators, operating systems (for example Berkeley UNIX 4.3BSD), computer algebra systems, and programming languages (for example C99).

In addition to base e, the IEEE 754-2008 standard defines similar exponential functions near 0 for base 2 and 10: $2^{x}-1$ and $10^{x}-1$.

A similar approach has been used for the logarithm (see lnp1).

An identity in terms of the hyperbolic tangent, $$\operatorname {expm1} (x)=e^{x}-1={\frac {2\tanh(x/2)}{1-\tanh(x/2)}},$$ gives a high-precision value for small values of x on systems that do not implement expm1(x).

See also

• Carlitz exponential, a characteristic p analogue
• Double exponential function – Exponential function of an exponential function
• Exponential field – Mathematical field with an extra operation
• Gaussian function
• Half-exponential function, a compositional square root of an exponential function
• Lambert_W_function#Solving_equations – Multivalued function in mathematics - Used for solving exponential equations
• List of exponential topics
• List of integrals of exponential functions
• Mittag-Leffler function, a generalization of the exponential function
• p-adic exponential function
• Padé table for exponential function – Padé approximation of exponential function by a fraction of polynomial functions
• Phase factor

External links

• "Exponential function", Encyclopedia of Mathematics, EMS Press, 2001 [1994]